【图】牟合方盖这神奇的几何奇特的方式令人惊讶

如果你是一个对数学非常感兴趣的人一定会对牟合方盖有一定了解，这是一种数学计算方法。数学一定是一个令许多人都感到非常痛苦与烦躁的科目，但是向牟合方盖这样的计算方法有非常的多，如果你对数学有一定兴趣可是要好好研究研究了。

牟合方盖

牟合方盖是由我国古代数学家刘徽首先发现并采用的一种用于计算球体体积的方法，类似于现在的微元法。由于其采用的模型像一个牟合的方形盒子，故称为牟合方盖。《九章算术》的"少广"章的廿三及廿四两问中有所谓"开立圆术"，"立圆"的意思是"球体"，古称"丸"，而"开立圆术"即求已知体积的球体的直径的方法。其中廿四问为:"又有积一万六千四百四十八亿六千六百四十三万七千五百尺。

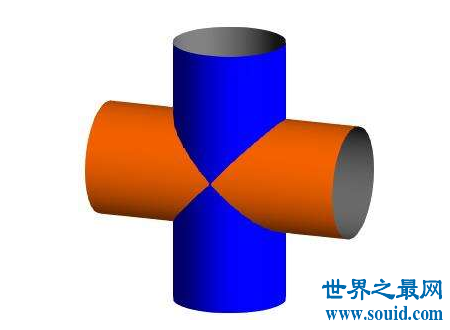
问为立圆径几何?开立圆术曰:置积尺数，以十六乘之，九而一，所得开立方除之，即丸径。"从中可知，在《九章算术》内由球体体积求球体直径，是把球体体积先乘16再除以9，然后再把得数开立方根求出约得14300尺，约为4.75米。是当一正立方体用圆柱从纵横两侧面作内切圆柱体时，两圆柱体的公共部分。刘徽在他的注中对其有以下的描述:"取立方棋八枚，皆令立方一寸，积之为立方二寸。

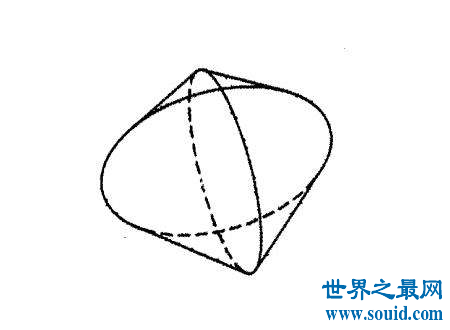
规之为圆囷，径二寸，高二寸。又复横规之，则其形似。八棋皆似阳马，圆然也。按合盖者，方率也。丸其中，即圆率也。"虽然本球体体积公式的出现比欧洲阿基米德的公式晚些，但由于方法以至推导都是由刘徽及祖氏父子自行创出，是一项杰出的成就。当中使用的"幂势既同，则积不容异。"，即"等高处截面面积相等，则二立体的体积相等。"的原理。

高数让人头痛难过

牟合方盖，什么东西，我看到只能表示一脸懵逼。不得不感叹啊，这个大学高数真是个复杂的东西啊，真的是源远流长啊，真的是什么都有啊，涉及广泛啊。大学高数这个原理是什么东西？不得不说的是，它是属于我国数学家的哦，是我国古代数学家刘徽发现的并采用的，是一种用于计算球体体积的方法，类似于现在的微元法。

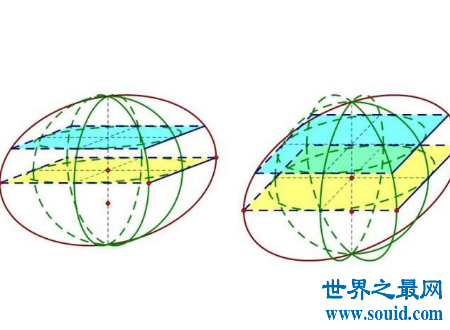
由于其采用的模型像一个牟合的方形盒子，所以它才叫牟合方盖。正因为它的模型是方形的，多用于求球的体积，所以它更多的是应用于工程数学上，我们都知道工程方面多用于模型嘛，而它就是最好的运用了，不仅有这样的模型，更能方便的求出球的体积，是工程上常用的方法。

是工程数学的重点内容。值得骄傲的是它是我国古代就有的计算早在中国数学典籍《九章算术》的“少广”章就有所谓的“开立圆术”。“立圆”的意思就是球体，而“开立圆术”即求已知体积的球体的直径的方法。

数学原理很是奇妙

如果你对数学很感兴趣那可要看看《数学原理》是由英国哲学家伯特兰·罗素(Bertrand Russell )和其老师怀特海(Alfred North Whitehead)合著的一本于1910-1913年出版的关于哲学、数学和数理逻辑的三大卷皇皇巨著，该书对逻辑学、数学、集合论、语言学和分析哲学有着巨大影响。正是这部巨著使罗素赢得了学术上的崇高地位和荣誉，

1949年罗素获得了英国的荣誉勋章。但是由于此书内容艰深，一般人，甚至专门从事数学原理探讨的人，也难以通读，所以，目前国内还没有完整的权威的中文译本。《数学原理》的主要目的是说明，所有纯数学都从纯逻辑前提推导的，并且只使用可以用逻辑术语定义的概念。